RSA常见解题方法汇总

一、RSA加解密参数生成

20240915212223

二、RSA加解密公式

加密公式

$$C = M^e\quad (mod\quad n)$$

解密公式

$$M = C^d\quad (mod\quad n)$$

三、九种常见题型解法思路

1. 已知p、q、 e， 求 d

$$e·d=1 (mod\quad \phi(n))$$

$$\phi(n) = (p-1)(q-1)$$

脚本： RSA1.py

import gmpy2
p = 38456719616722997
q = 44106885765559411
e = 65537

phi_n = (p-1)*(q-1)
d = gmpy2.invert(e,phi_n)
print("dec:" + str(d))
print("hex:" + hex(d))

2. 已知n，e 求d （其中n比较小）

先使用yafu将n分解，然后解法同1。（在线分解: www.factordb.com)

<笔者环境：yafu 在win7中安装>

#打开yafu命令行，输入
factor（n）

#n比较大时会报错，将n写入data.txt文件，再执行
factor(@) -batchfile data.txt

3. 已知公钥（n，e）和密文c，求明文m

场景一： n，e不太大

将n进行分解，然后解法同1方式计算m。

场景二： n，e比较大

用到RsaCtfTool脚本进行爆破。

<笔者环境：kali中的安装路径（～/Software/RsaCtfTool-master）>

（1）利用n，e生成pem公钥文件

python RsaCtfTool.py --createpub --n n的值 --e e的值 > pubKey.pem 

（2）使用公钥和密文进行爆破

python RsaCtfTool.py --publickey pubKey.pem --uncipherfile cipher.enc

4.已知密文文件 flag.enc / cipher.bin / flag.b64 和公钥文件 pubKey.pem / key.pub，求明文：m

其中 '/' 代表 '或'

方法一： 使用公钥爆破

公钥文件或密文文件正常编码时，直接使用RsaCtfTool工具爆破，如果公钥文件或密钥文件进行过base64编码需要解码成正常编码的文件，然后进行爆破

python RsaCtfTool.py --createpub --n n的值 --e e的值 > pubKey.pem

方法二： 公钥转成私钥后爆破

（1）在公钥文件pubKey.pem中提取n的值(Modulus为n的值，Exponent为e的值)

openssl rsa -pubin -text -modulus -in pubKey.pem

20240915213511

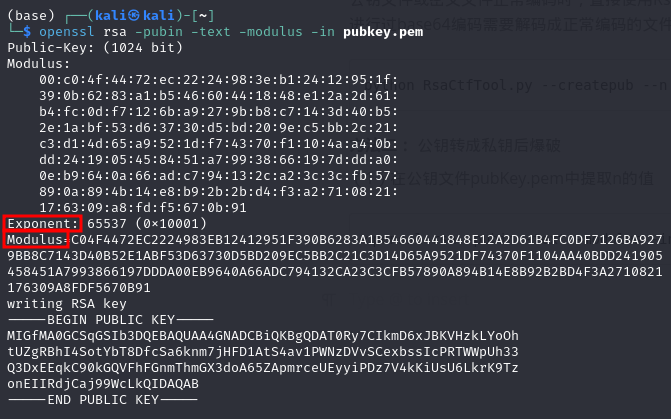
（2）对n进行分解，得到p，q

使用yafu或在线分解工具（www.factordb.com）

（3）使用e，p，q生成私钥

python RsaCtfTool.py -o priKey.pem -e e的值 -p p的值 -q q的值

（4）使用私钥爆破解密密文

#使用openssl命令
openssl rsautl -decrypt -in flag.enc -inkey priKey.pem

#或者使用RsaCtfTool脚本
python RsaCtfTool.py --private priKey.pem --uncipherfile flag.enc

5.已知c，e，n（非常大），和dp，dq，求解明文m

$$dp=d(mod(p-1)) \\\ \\\ dq=d(mod(q-1))$$

import gmpy2
import libnum

e = 65537
n = XXXX
dp = XXXX
c = XXXXX

for i in range(1,65538):
    if (dp*e-1)%i == 0:
        if n%(((dp*e-1)//i)+1) == 0:
            p = ((dp*e-1)//i)+1
            q = n//(((dp*e-1)//i)+1)
            phi = (p-1)*(q-1)
            d = gmpy2.invert(e,phi)%phi
            print(libnum.n2s(pow(c,d,n)))

6.已知n（非常大），e，d求p，q

p，q无法通过分解n直接求得

解题脚本： RSA2.py

关键点在于求出p，q

import random
from md5 import md5
import libnum

def getpq(n,e,d):
    p = 1
    q = 1
    while p == 1 and q == 1:
        k = d * e - 1
        g = random.randint(0,n)
        while p == 1 and q == 1 and k % 2 == 0:
            k /= 2
            y = pow(g,k,n)
            if y != 1 and libnum.gcd(y-1,n)>1:
                p = libnum.gcd(y-1,n)
                q = n/p
    return q,p


def main():
    n = XXX
    e = XXX
    d = XXX
    p,q = getpq(n,e,d)
        print p
        print q
        print("Flag:flag{%s}" %md5(str(p+q)).hexdigest()

if __name__ == '__main__':
    main()

7.提取私钥中的信息

python RsaCtfTool.py --key private.pem --dumpkey

8.利用公钥文件生成私钥文件

python RsaCtfTool.py --publickey pubkey.pem --private > private.pem

9.n分解出多个不同的因子时，求明文m

$$n = x * y * z \\\ \\\ \phi(n)=\phi(x*y*z)\\\ \quad \quad \quad \quad \quad=\phi(x)*\phi(y)*\phi(z)\\\ \quad \quad \quad \quad \quad \quad \quad =(x-1)(y-1)(z-1)$$

import gmpy2
from Crypto.Util.number import long_to_bytes

n=54418730685090279762910735361926
e = 65537
c = 439254892838483084823049210948379283948292882203048278474729374
p1 = 738273837282
p2 = 327283728378233
p3 = 283839239472971839
phi_n = (p1-1)*(p2-1)*(p3-1)
d = gmpy2.invert(e,phi_n)
m = gmpy2.powmod(c,d,n)
print(long_to_bytes(m))